Representation-Based Exploration for Language Models:
From Test-Time to Post-Training

Jens Tuyls1, Dylan J. Foster2, Akshay Krishnamurthy2, Jordan T. Ash2
1Princeton University, 2Microsoft Research NYC
[Paper] [Code (Coming Soon)] [Data (Coming Soon)]

Inference-Time Exploration

Teaser inference-time

Exploration for RL Post-Training

Teaser post-training

Abstract

Reinforcement learning (RL) promises to expand the capabilities of language models, but it is unclear if current RL techniques promote the discovery of novel behaviors, or simply sharpen those already present in the base model. In this paper, we investigate the value of deliberate exploration—explicitly incentivizing the model to discover novel and diverse behaviors—and aim to understand how the knowledge in pre-trained models can guide this search. Our main finding is that exploration with a simple, principled, representation-based bonus derived from the pre-trained language model's hidden states significantly improves diversity and pass@k rates—both for post-training, and in a novel inference-time scaling setting we introduce.

  1. For inference-time, exploration with representation-based diversity improves efficiency, consistently improving pass@k rates across a variety of models and reasoning tasks. For example, for Qwen-2.5-14b-Instruct we obtain over 50% improvement in verifier efficiency on almost all tasks.
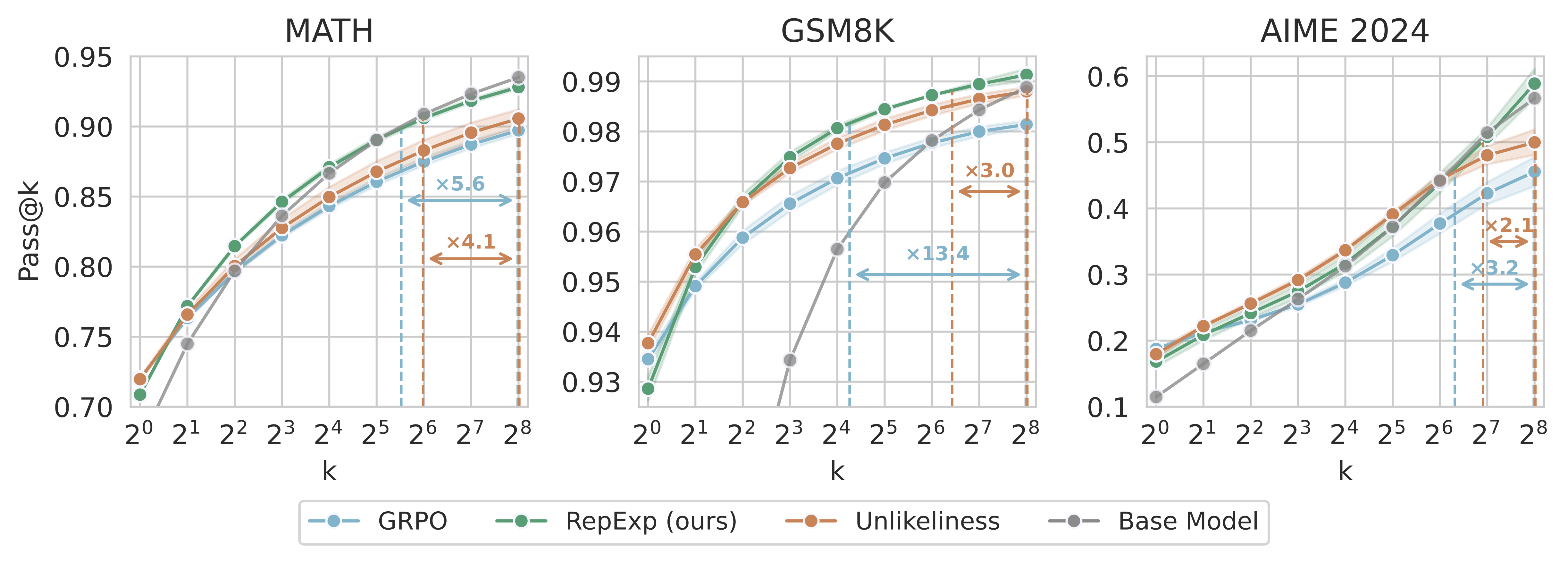
  2. For post-training, we show that integrating this exploration strategy into an RL pipeline improves reasoning performance over that of the initial model and over standard RL post-training. For example, on AIME 2024, our post-trained Qwen-2.5-7b-Instruct's pass@80 matches the pass@256 of GRPO on the same model, demonstrating a 3x improvement in test-time sample efficiency.

Overall, our findings suggest that deliberate exploration—with the right notion of diversity—is a practical path toward discovery of new behaviors beyond sharpening.

Representation-Based Exploration: Inference-Time and RL

We focus our experiments on a simple, principled exploration strategy: an adaptation of elliptic bonuses and sampling — a de facto standard for linear bandits and active learning — with a representation derived from the language model's hidden states.

At a high level, elliptical bonus methods operate over a $d$-dimensional feature space and adopt a linear-algebraic measure of novelty: given previously seen feature vectors $h_1, \ldots, h_{i - 1}$, the novelty (or bonus) of a new feature vector $h$ is defined as:

\[ \text{div}(h | h_{1:i - 1}) = h^T \Sigma_i^{-1} h \quad \Sigma_i = \lambda I_d + \Sigma_{j < i} h_j h_j^T \]

To adapt elliptical bonuses to language models, we use representations extracted from the model itself as the feature vectors. Formally, given a prompt $x$ and a response $y_i=y_i^1,\ldots,y_i^T$ of $T$ tokens, we form the feature vector as $\bar{h}_\theta(x,y_i) := \frac{1}{T}\sum_{t=1}^T h_\theta(x,y_i^{1:t})$ where $h_\theta(x,y_i^{1:t})\in \mathbb{R}^d$ is the last-layer hidden state of the model on input $(x,y_i^{1:t})$ (the activation prior to the unembedding matrix).

Representation-based exploration for inference-time selection. The figure below presents RepExp, our main algorithm for inference-time selection using representation-based elliptical bonuses. Here, given a single prompt $x$ and a set of candidate generations $\mathcal{Y} = \{y_1, \ldots, y_N\}$, we iteratively select the generation that maximizes the elliptical bonus via:

\[ y_{t + 1} = \underset{y \in \mathcal{Y}}{\mathrm{argmax}}\, \bar{h}_\theta(x, y) \Sigma_t^{-1} \bar{h}_\theta(x, y). \]
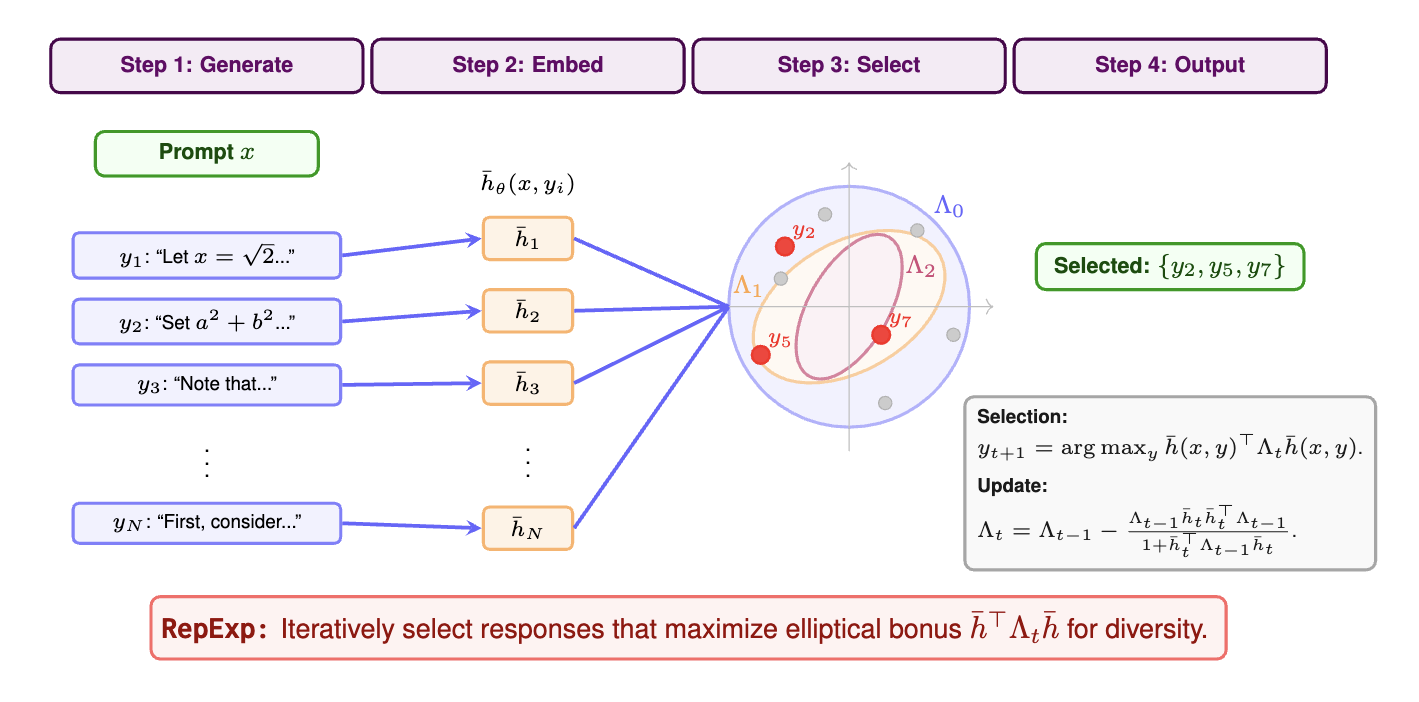
RepExp for inference-time exploration
RepExp for inference-time exploration. Given a prompt, RepExp selects a diverse set of responses from a large pool by optimizing elliptical bonuses computed using representations from the language model.

Representation-based exploration for RL post-training. For our post-training experiments, we use the same representations $\bar{h}_\theta(x, y)$ as above, but directly augment the rewards with elliptic bonuses instead of performing coreset selection. Concretely, given the current iterate $\pi_\theta$ in GRPO, we first sample a group of $k$ responses $y_1, \ldots, y_k \overset{\textrm{i.i.d.}}{\sim} \pi_\theta(\cdot | x)$ for each prompt $x$. Letting $\Sigma := \lambda I_d + \Sigma_{i = 1}^k \bar{h}_\theta(x, y_i) \bar{h}_\theta(x, y_i)^T$, we define the reward for response $y_i$ as:

\[ r^*(x, y_i) + \beta \cdot \bar{h}_\theta(x, y_i) \Sigma^{-1} \bar{h}_\theta(x, y_i), \]

where $\beta > 0$ is a bonus parameter.

Why representation-based elliptical bonuses? First, by leveraging the hidden state of the model in featurization, the bonuses capture rich information about the generations, thereby incorporating the language model's prior knowledge. Second, the method is history-aware: the covariance matrix summarizes all previously selected generations, and redundancy with previous selection (in representation space) is penalized. Finally, the method is simple and scalable, involving no additional learning machinery and using rank-one updates to avoid costly matrix inversions.

Inference-Time Exploration: Experimental Results

We present our results as a series of Research Findings (RF).

RF #1: RepExp improves verifier efficiency across models and tasks.

RF #1: Representation-based inference-time exploration improves verifier efficiency.
Representation-based inference-time exploration improves verifier efficiency. (Left) We plot the samples-to-correct, the average number of samples until a correct response is selected, for a wide range of tasks and models. We compare two inference-time exploration methods: representation-based exploration and naive (random) sampling from the base model. (Right) We display samples-to-correct, disaggregated to each question in the dataset, for two model-task pairs. We find representation-based exploration improves over random sampling for most model-task pairs. For example, for Qwen-2.5-14b-Instruct we obtain over 50% improvement in verifier efficiency on GSM8K, MATH, MBPP+, and Game-of-24.

RF #2: The benefits of RepExp grow with model strength.
RF #3: RepExp provides more improvement for harder questions.

RF #2 & #3: The benefits of RepExp grow with model strength. RepExp provides more improvement for harder questions.
A closer look into when RepExp provides improvement. (Left) For each task, we rank models according to their pass@1 rate (the weakest model has rank 0, and the strongest has rank 8). We then plot relative improvement (%) of RepExp over random sampling, sorting by rank on the x-axis. While RepExp can hurt weaker models (e.g., Qwen-2.5-0.5B-Instruct), we find stronger models almost always benefit from exploration (e.g., Qwen-2.5-14B-Instruct). (Right) For two different model-task pairs, we plot the samples-to-correct as a function of question hardness. Hardness is measured by the samples-to-correct from a high-quality third-party model (GPT-4o mini). We find that RepExp has the greatest benefit on harder examples (e.g., the hardest 20% of questions on MATH). Shaded areas indicate one standard error.

RF #4: RepExp improves verifier efficiency across models and tasks.

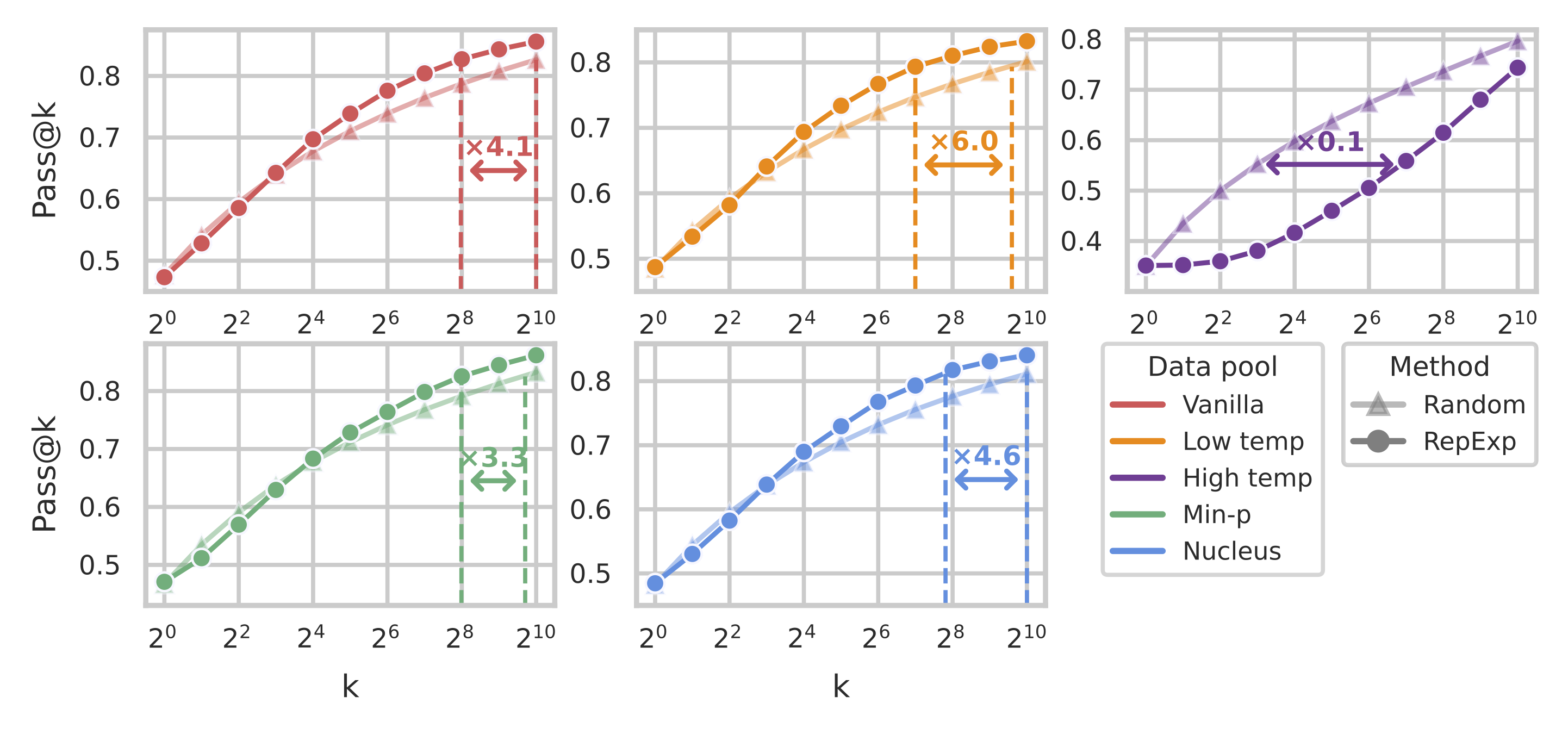
RF #4: Benefits of RepExp across data pools.
Benefits of RepExp across data pools, for the inference-time exploration setup in RF #1. We plot the pass@k curve for random vs. RepExp across five different data pools (base samplers). RepExp on top of vanilla generation outperforms random sampling on top of any of the generation strategies. Moreover, except for the high-temperature pool, RepExp over a pool improves verifier efficiency, with 3x to 6x improvement over random sampling for that pool.

RF #5: RepExp for autoregressive generation improves solve rate.

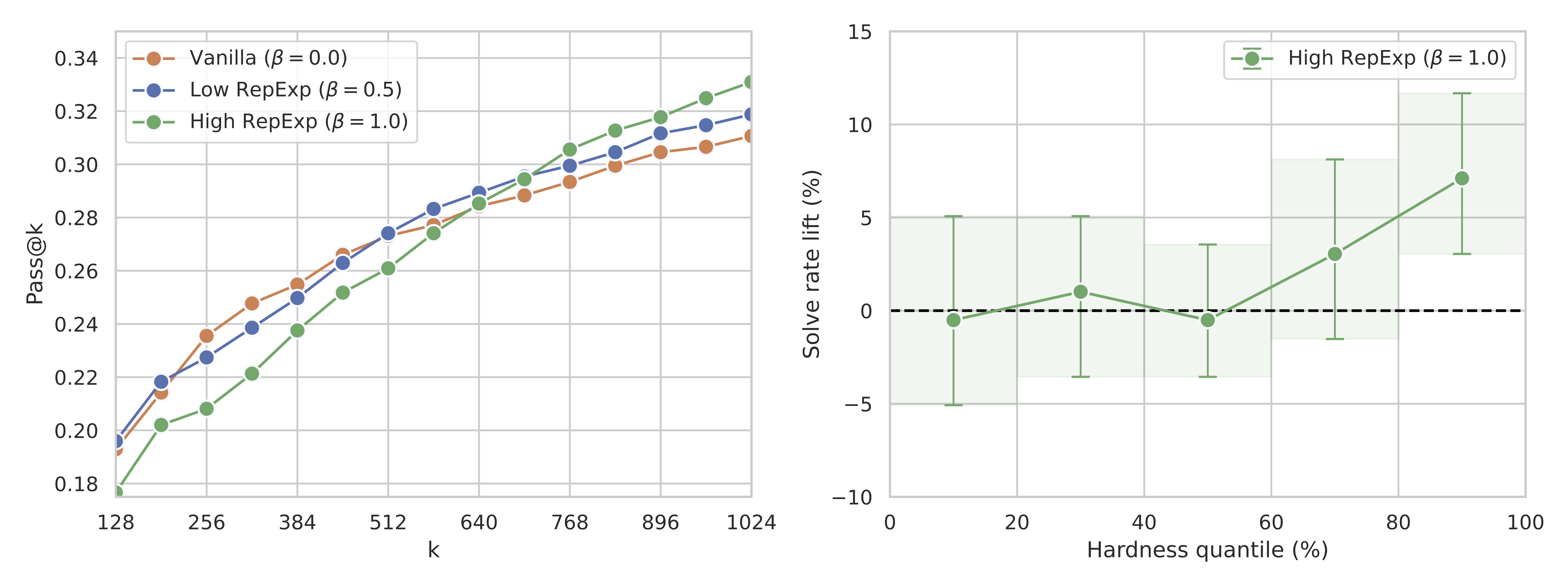
RF #5: RepExp for autoregressive generation improves solve rate.
Representation-based exploration at the token level, compared to naive autoregressive generation ($\beta=0$) for inference-time exploration. (Left) We plot pass@k for different exploration methods on Qwen-2.5-7B-Instruct, for the 200 hardest (but solvable) questions in MATH as judged by GPT-4o-mini. RepExp improves pass@k for large $k$ over naive sampling (for both choices of $\beta$). (Right) When binning the questions by hardness (judged by samples-to-correct for GPT-4o-mini), solve rate improves the most on the hardest questions. Error bars indicate 95% paired bootstrap CIs.

Exploration for RL Post-Training

RF #6: RepExp improves pass@k.

RF #6: RepExp improves pass@k.
Pass@k for RL post-training with exploration. We find that RL generally increases the pass@k for small values of $k$ compared to the base model, but that exploration is required to improve or even preserve base model pass rates for larger values of $k$. For MATH and GSM8K, RepExp roughly matches or improves upon Unlikeliness for $k \ge 2$. For AIME 2024, RepExp is slightly worse than Unlikeliness until $k = 64$, after which it surpasses Unlikeliness for all larger values of $k$. Shaded areas indicate one standard error. Horizontal arrows indicate the test-time sample efficiency improvement for pass@256 of RepExp over GRPO (blue) and Unlikeliness (orange). RepExp is 2.1-4.1x more sample-efficient than Unlikeliness and 3.2-13.4x more sample-efficient than GRPO.